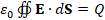
(A.1) ε_0 ∯▒〖E∙dS=Q〗

Fig. 80. Testing of Gauss’s law using much intermediate matter.

Fig. 81. Gravitational force points inward toward gravitating mass.
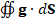
(A.6) ∯▒〖g∙dS〗 = -M
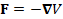
(A.7) F=-∇V

(A.8) work done = ∫_(initial point)^(final point)▒〖F∙dx〗

(A.9) ∮_(closed path)▒〖F∙dx〗= ∬_(bounded by closed path)▒〖(∇×F)∙dS〗 =0
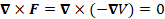
(A.10) ∇×F=∇×(-∇V)=0
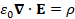
(A.17) ε_0 ∇∙E=ρ ... (A.21) ε_0 ∇∙E=ρ
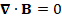
(A.18) ∇∙B=0 ... (A.22) ∇∙B=0
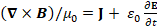
(A.19) (∇×B)/μ_0=J+ ε_0 ∂E/∂t
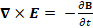
(A.20) ∇×E= -∂B/∂t
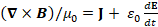
(A.23) (∇×B)/μ_0=J+ ε_0 dE/dt
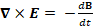
(A.24) ∇×E= -dB/dt
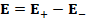
(A.25) E=E_+-E_-
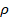
densities, ρ, ... with ρ being zero
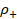
Note that ρ_+ and
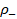
and ρ_- are both nonnegative.
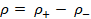
(A.26) ρ= ρ_+- ρ_-
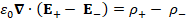
(A.27) ε_0 ∇∙(E_+- E_- )=ρ_+- ρ_-
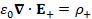
(A.28) ε_0 ∇∙E_+=ρ_+
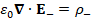
(A.29) ε_0 ∇∙E_-=ρ_-
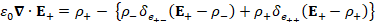
(A.30) ε_0 ∇∙E_+=ρ_+- {ρ_- δ_(e_(+-) ) (E_+-ρ_- )+ρ_+ δ_(e_(++) ) (E_+-ρ_+ )}
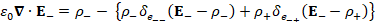
(A.31) ε_0 ∇∙E_-=ρ_-- {ρ_- δ_(e_(--) ) (E_--ρ_- )+ρ_+ δ_(e_(-+) ) (E_--ρ_+ )}
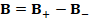
(A.32) B=B_+-B_-
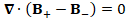
(A.33) ∇∙(B_+-B_- )=0
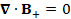
(A.34) ∇∙B_+=0
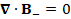
(A.35) ∇∙B_-=0
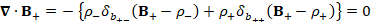
(A.36) ∇∙B_+=- {ρ_- δ_(b_(+-) ) (B_+-ρ_- )+ρ_+ δ_(b_(++) ) (B_+-ρ_+ )}=0
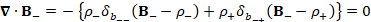
(A.37) ∇∙B_-=- {ρ_- δ_(b_(--) ) (B_--ρ_- )+ρ_+ δ_(b_(-+) ) (B_--ρ_+ )}=0
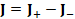
(A.38) J=J_+-J_-
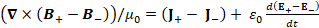
(A.39) (∇×(B_+-B_- ))/μ_0=(J_+- J_- )+ ε_0 d(E_+-E_- )/dt
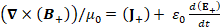
(A.40) (∇×(B_+ ))/μ_0=(J_+ )+ ε_0 d(E_+ )/dt
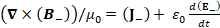
(A.41) (∇×(B_- ))/μ_0=(J_- )+ ε_0 d(E_- )/dt
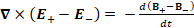
(A.42) ∇×(E_+-E_- )= -d(B_+-B_- )/dt
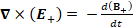
(A.43) ∇×(E_+ )= -d(B_+ )/dt
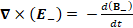
(A.44) ∇×(E_- )= -d(B_- )/dt
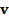
The “v” becomes the velocity
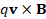
The qv×B portions are not needed ... was previously modelled continuously by qE+qv×B.
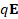
, and absorption information in qE. The full qE information contains
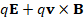
was previously modelled continuously by qE+qv×B.
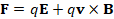
(A.45) F=qE+qv×B
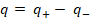
(A.46) q= q_+- q_-
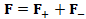
(A.47) F=F_++F_-
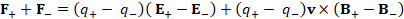
(A.48) F_++F_-=(q_+- q_- )( E_+-E_- )+(q_+- q_- )v×(B_+-B_- )
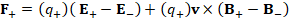
(A.49) F_+=(q_+ )( E_+-E_- )+(q_+ )v×(B_+-B_- )
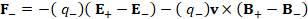
(A.50) F_-=-( q_- )( E_+-E_- )-( q_- )v×(B_+-B_- )
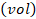
over the volume (vol) of a
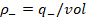
charges and the densities, ρ_-=q_-/vol
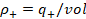
and ρ_+=q_+/vol, assuming for the moment
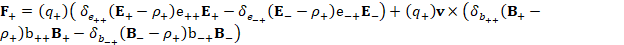
(A.51) F_+=(q_+ )( 〖δ_(e_(++) ) (E_+-ρ_+ )e〗_(++) E_+-〖〖δ_(e_(-+) ) (E_--ρ_+ )e〗_(-+) E〗_- )+(q_+ )v×(〖〖δ_(b_(++) ) (B_+-ρ_+ )b〗_(++) B〗_+-〖δ_(b_(-+) ) (B_--ρ_+ ) b_(-+) B〗_- )
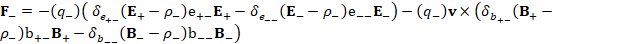
(A.52) F_-=-(q_- )( 〖δ_(e_(+-) ) (E_+-ρ_- )e〗_(+-) E_+-〖〖δ_(e_(--) ) (E_--ρ_- )e〗_(--) E〗_- )-(q_- )v×(〖〖δ_(b_(+-) ) (B_+-ρ_- )b〗_(+-) B〗_+-〖〖δ_(b_(--) ) (B_--ρ_- )b〗_(--) B〗_- )
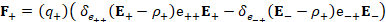
(A.53) F_+=(q_+ )( 〖δ_(e_(++) ) (E_+-ρ_+ )e〗_(++) E_+-〖〖δ_(e_(-+) ) (E_--ρ_+ )e〗_(-+) E〗_- )
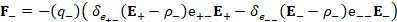
(A.54) F_-=-(q_- )( 〖δ_(e_(+-) ) (E_+-ρ_- )e〗_(+-) E_+-〖〖δ_(e_(--) ) (E_--ρ_- )e〗_(--) E〗_- )
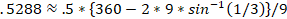
A half degree is about .5288≈.5*{360-2*9*〖sin〗^(-1) (1/3)}/9 or half the average available angular gap

Fig. 82. Rendition of Bessler's final figure showing half degree line width.

Fig. 83. Seer lobe rolls without slipping over its lobe-hole.

Fig. 84. Shows the initial geometry of the roller bearing.

Fig. 85. My Orffyreum final figure in Apologia.
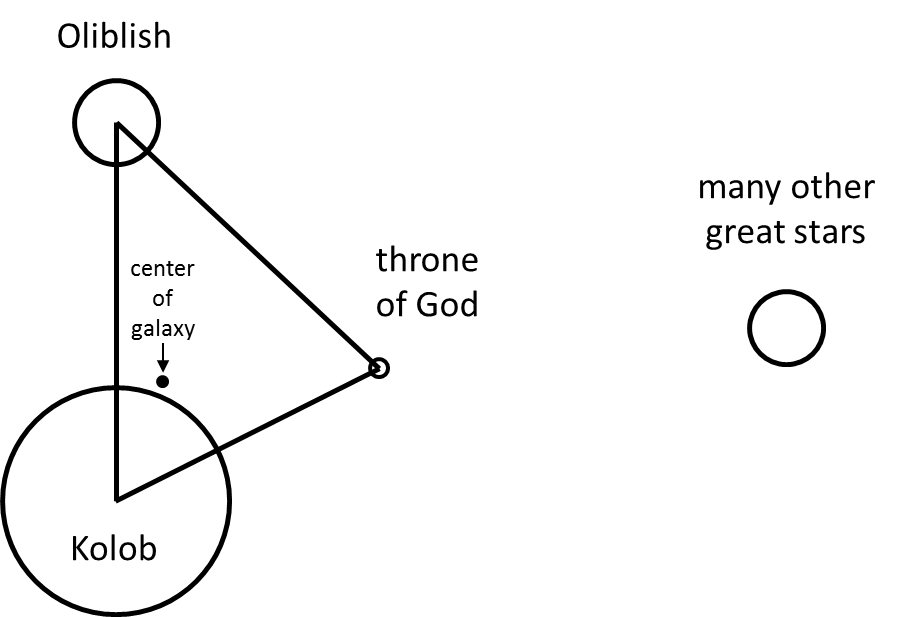
Fig. 86. Relationship between Kolob, Oliblish, and the throne of God.

Fig. 87. Yin-yang rotation about horizontal axis, sans dots.

Fig. 88. Yin-yang rotation about horizontal axis, showing dots.

Fig. 89. Sprocket wheels for ED.L.'s Sweet Sixteen family of cylinders.
Return to Main Page