
Fig. 20. Orthogonal offset constraint for absorption of first absorbed electric field by charge q.
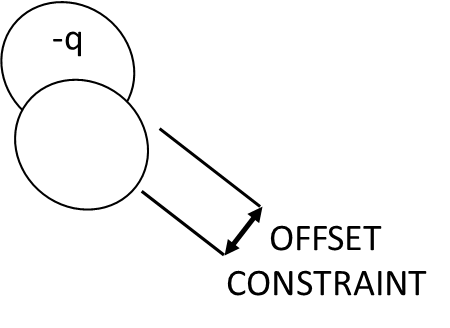
Fig. 21. Offset constraint for absorption of second absorbed electric field by charge -q.
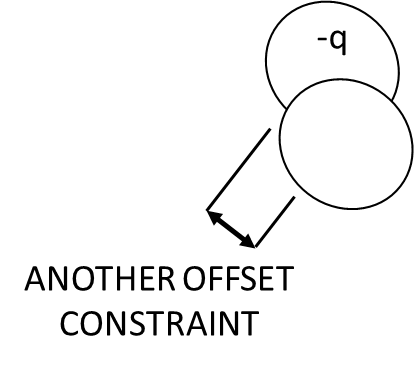
Fig. 22. Orthogonal offset constraint for absorption of second absorbed electric field by charge -q.
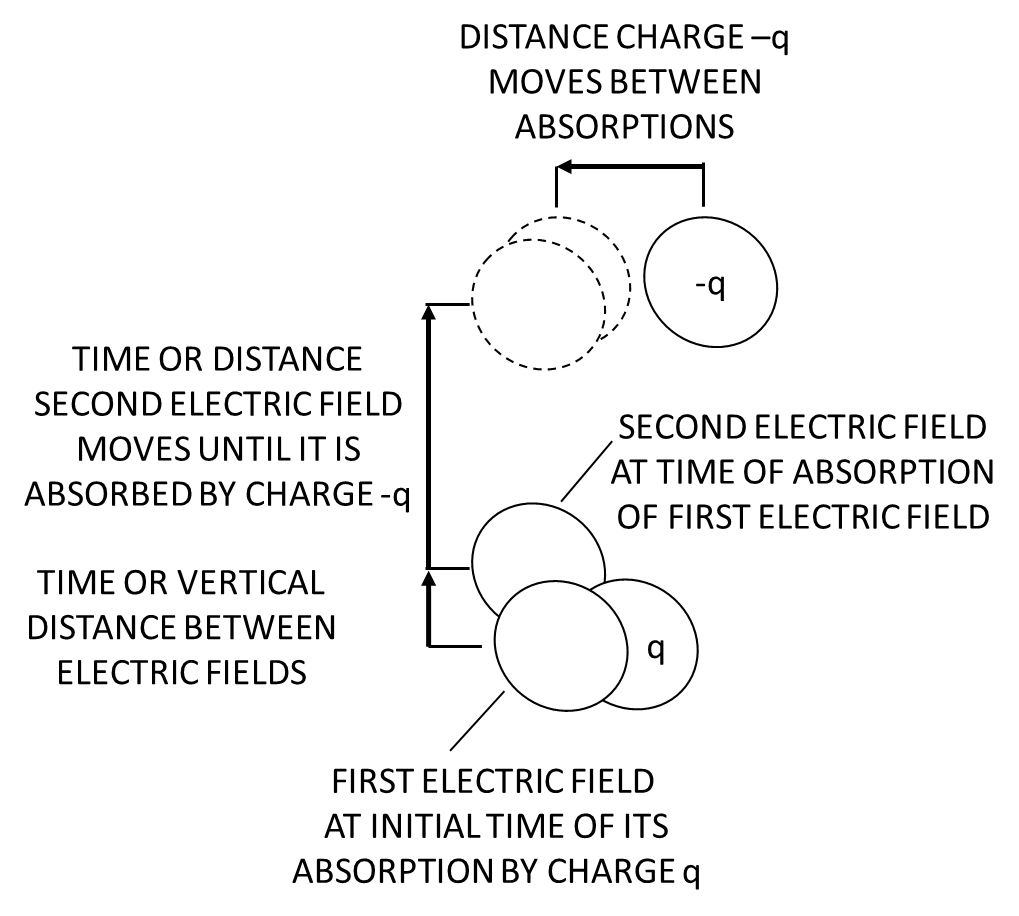
Fig. 23. Timing offset constraint for absorption of second absorbed electric field.
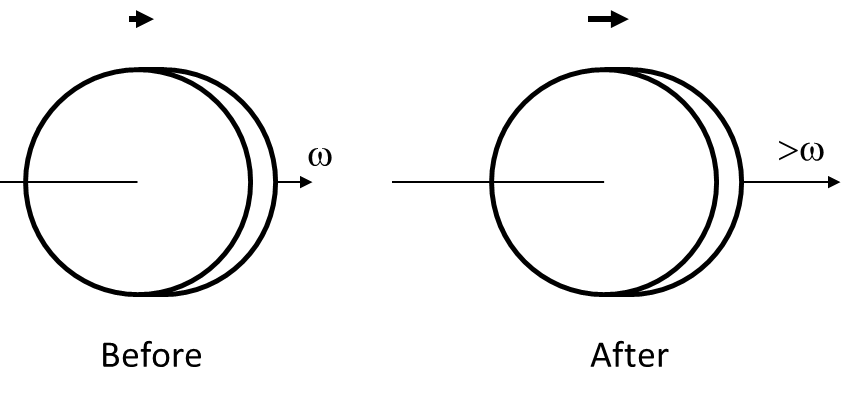
Fig. 24. Macro illustration of the Bessler principle.
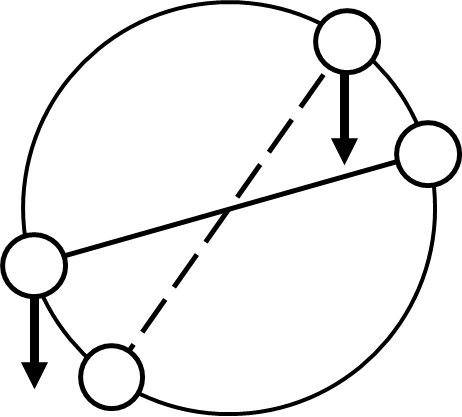
Fig. 25. Micro illustration (left-right) of Bessler principle.

Fig. 26. Micro illustration (left-left) of Bessler principle.
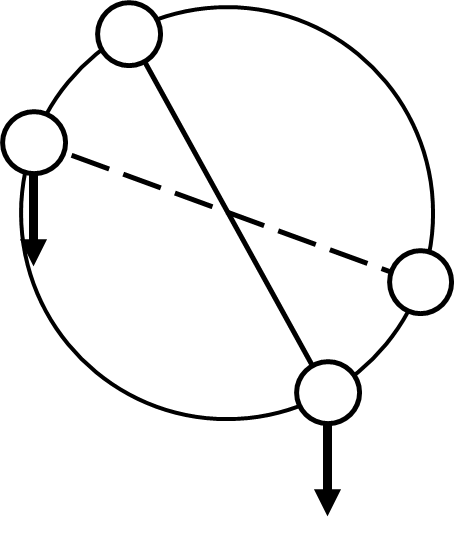
Fig. 27. Micro illustration (right-left) of Bessler principle.
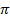
within "3.2 Example Bessler Principle Calculation" ... y1(t) = r*sin(2π*f*(t- ti) + 3π/2) ... x1(t) = r*cos(2π*f*(t- ti) + 3π/2). ... circumference is π *2, ... y2(t) = r*sin(2π*f*(t- ti) + 3π/2 - π), ... x2(t) = r*cos(2π*f*(t- ti) + 3π/2 - π). ... around the circle by some angle, θ = 2π*(tf-ti)*f, ... about the origin of r*F*sin(θ) = r*F*sin(2π*(tf-ti)*f) ... within "5.1 Atmospheric or Orbital Phenomena" ... area on the surface of a sphere of radius r is S = 4πr2 = 4πr*r and the area of a circle of radius r is A = πr2 = πr*r ... the surface (4π*D*D) of that sphere except for an area corresponding to the area presented by the sun (π*s*s). ... an area of 4π*D*D - π*s*s. On that large sphere of radius D, there would be a temperature of 6000°K assigned to an area of π*s*s. The sum of those two areas is 4π*D*D. ... (5.1) a = {6000°K*π*s*s + 3°K*(4π*D*D - π*s*s)}/{4π*D*D} ... within "Ball Lightning" ... We see that (surface area)/volume = (4πr2)/((4/3)πr3) = 3/r is larger when r is smaller. ...
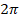
...
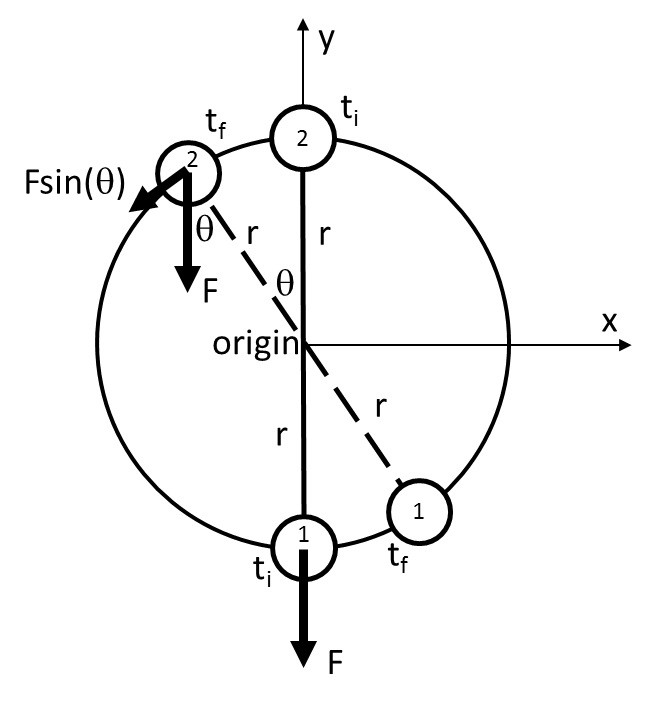
Fig. 28. Illustration for calculation of Bessler principle.
Fig. 29. Railroad Wheels.
Return to Main Page